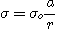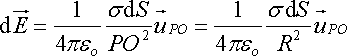Exercise Pro

►Back to the Exercise Field created by a portion of a cone. The planes passing through the axis Ox are the charge distribution of planes of symmetry. The electrostatic field must belong simultaneously to all of these plans therefore their intersection: the field has its direction carried by the axis Ox Consider a surface element S on the truncated cone centered about the point P. The figure in the plane of the sheet is as follows: This surface element creates an elementary field O: Only the projection of this vector onto axis Ox contributes to the field at the point O: L is expressed as a function of r: We get : The field O is: ►Back to exercise ►See the list of exercises       

► see solution Field created by a portion of a cone. Consider a portion of a cone of half-angle at the apex a and R1 limit rays and R2 (R1 <R2). This system is loaded on the surface with non-uniform density: . a is a constant homogeneous to a length and r the radius of the cone at a point on its axis of symmetry. Determine the electrostatic field at the top of the cone O. ► see solution ►See the list of exercises  

►Back to exercise 1. O electrostatic field. The z axis is the axis of symmetry of load distribution. Field O is carried by this axis. Consider a surface element of the half sphere centered at a point P. Elemental electrostatic field created by this element to the point O of the axis Oz is expressed as: Only the projection of this vector onto axis Oz contributes to the field at the point O: The field component O is: 2. Electrostatic Field in M. The z axis is the axis of symmetry of load distribution. The field M is carried by this axis. Consider a surface element of the half sphere centered at a point P. Elemental electrostatic field created by this element at the point M of the axis Oz is expressed as: Only the projection of this vector onto axis Oz contributes to the field at point M: Gold : and where: By integration: Gold : ...

► see solution Field generated by a hemisphere surface charge. Considering a half sphere of center O, of radius R, uniformly charged surface with the surface density s. 1. Determine the electrostatic field at the point O. 2. In the same issue in a point M of the axis Oz of symmetry of this hemisphere. Find the result of Question 1. ► see solution ►See All the list of the Exercises  

►Back to exercise Field at the center of a loaded ring having an opening. And the xOy plane xOz are planes of symmetry of the distribution of loads, the electrostatic field must belong simultaneously to these two planes, so they intersect. The field at the point O is then carried by the right Ox. Either elemental electrostatic field created by the length dl element centered at a point P on the charged circumference of the ring: Given the symmetry of the charge distribution, only the component along Ox contributes to total field O. Where: The resulting field component for O: ►Back to exercise ►See the list of exercises

► See solution A ring center O and radius R bears a uniform linear charge density λ except on a corner arc center 2α Determine the electrostatic field in O. ► See solution ►See the list of electromagnetism exercises

► E lectrostatic field . ∎ 1. Field the center of a ring having an opening. (The solution ) ∎ 2. Field created by a hemisphere surface charge. ( The Solution ) ∎ 3. field created by a portion of a cone. (The Solution ) ∎ 4. Field created by a disc at a point on its axis. (The Solution ) ∎ 5. electrostatic field created by an electrified segment. (The solution ) ∎ 6. Electrostatic field created by a hemisphere surface charge. ( The solution ) ∎ 7. Electric field on the axis of a system (-q, + q) ( the solution )     ►2. Electrostatic potential . ∎ 1. The potential field created by a disc at a point on its axis of revolution . ~ ∎ ( The Solution ) ∎ 2. Potential and field created by a charged hemisphere surface ~ ∎ ( the solution ) ∎ 3. The potential created by a portion of a cone ~ ∎ ( The solution ) ∎ 4. Field Lines ► 3. Gauss Theorem ∎ 1. Hydrogen Atom ~ ∎ ( T he solution ) ∎ 2. Study of a cylindrical charge ...