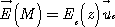Exercise Pro

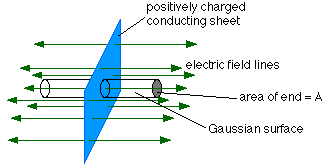
∎ 1. Hydrogen Atom ~ ∎ ( The solution ) ∎ 2. Study of a cylindrical charge distribution. ~ ∎ ( The solution ) ∎ 3. Crossing a charged layer ~ ∎ (The solution ) ∎ 4. Field on the axis of a circular opening of a plan. ~ ∎ ( The Solution ) ∎ 5. Field in a spherical cavity. ~ ∎ ( The solution ) ∎ 6. Research Officer of the electrostatic field generated by a half-charged sphere surface. ∎ 7. Study of a spherical inhomogeneous distribution. ~ ∎ ( The Solution ) ∎ 8. field in the vicinity of the axis of a uniformly charged hoop ~ ∎ ( The Solution ) ∎ 9. uniform volumetric density between two planes ► See the list of electromagnetism corrected exercises

Consider two infinite planes x = - a and x = a. The space between the two planes has a volume density of uniform and constant ρ loads. For x> a and x <- a, it reigns on vacuum . Show that at any point of space, the electrostatic field of this distribution can be written . Expressing Ex for the different parts of space and plot the Ex a function of x. Determine for each region the potential V (x) adopting V (0) = 0. Draw the graph of V (x) in terms of x. It is assumed that a approaches 0 and that the multiplication  ρa remains finite. Set an areal density limit load and look for Ex   on a classic result. ► See solution ► See the list of electromagnetism exercises

► Return to the exercise 1. electrostatic field at a point on the axis of the ring. The planes containing the axis Oz are symmetry planes of load distribution  ; at a point M of this axis, the direction of the electrostatic field must belong to each plan so they intersect: with So: where: As the plane containing the hoop is also a load distribution of the symmetry plane was at a point M' is symmetrical of M from the hoop:       with: Finally, we get to any point on the axis of the hoop: 2. Field in a spot close to the axis. We work in cylindrical coordinates. For any point M of space, the plane containing the point M and the axis Oz is a plane of symmetry of the charge distribution. The field is contained in the plan. Furthermore as there invariance of the charge distribution by rotation about axis Oz we ...

►See the solution A hoop of radius R, center O, carries the linear  uniform load λ . 1.         Determining the expression of the electrostatic field created by the hoop at a point M of the axis Oz. 2.         It is proposed to calculate now the field in the vicinity of the axis of the hoop. Using a Gaussian surface having the form of a small Oz axis of cylinder of radius r and of length dz and by assuming that E z (r, z) = E z (axis) to a point close to the axis, show that the radial component of the field is related to the value of the field axis by: Determine at a point closest to the axis. ►See the solution ► See the list of electromagnetism exercises