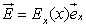Exercise Pro

∎ Return to the exercise 1. Expression of the electrostatic field.   All the planes containing the center O of the sphere and the point P are the load distribution of planes of symmetry. The electric field must belong simultaneously to all of these plans, it is therefore carried by their intersection which is the line OM.  we obtain.: As this distribution has a rotational invariance around the point O, the electric field does not depend on the angular variables. This result does not depend on the position of this point P. We choose a Gaussian surface centered in O and radius r. The Gauss theorem is: Then there are two regions of space: ● For r <R (one can put an equal sign here because the density distribution is what ensures the continuity of the normal component (here radial) of the electrostatic field). For the domestic load: Is obtained by applying the Gauss theorem: ...

►Voir solution Considering in the vacuum a sphere of radius R, the center O, with a volume charge distribution : and k are constants and 1. Determine the expression of the electrostatic field at any P in space. Note OP = r. 2. Show that within the sphere, the electrostatic field has a maximum for a ratio r / R given. Calculate the value of k in the case where the field is extremum for r / R = 1/2 ►Voir solution ∎ See the list of electromagnetism corrected exercises  

Considering a half sphere of center O, of radius R, uniformly charged surface with the surface density s. Determine, using only the symmetries The invariance, the Gauss theorem and the superposition principle the direction of the electrostatic field at any point M of the diametrical plane.   ∎ solution soon ∎ See the list of electromagnetism exercises

∎ Return to the exercise   We Can modeled within a cavity hollowed out of the sphere R as the superposition of a charged sphere of radius a volume density - ρ   of center O2 and a full sphere of volume density ρ of radius R and center O1. The principle of superposition is applied at a point M of the cavity: field created by the distribution ρ field created by the distribution - ρ Symmetry and invariance of each source can be concluded for each radial field : Using the Gauss, taking for each distribution a sphere of radius r and center Oi closed surface and passing through the point M.   We get : The field is uniform at any point inside the cavity. ∎ Return to the exercise ∎ Back to the list of electromagnetism corrected exercises

►Voir solution A sphere of radius R, carrying a load volume r that is uniformly distributed throughout the volume which occupies  the exception of a radius of cavity a. The center of this cavity is the distance of the center of the sphere. The cavity is empty loads. Using the Gauss theorem and the principle of superposition, calculate the field at all points of the cavity.   what is remarkable? ►Voir solution ∎ See the list of electromagnetism exercises

∎ Back to exercise     The Load distribution can be seen as the result of the superposition of an infinite plane of a surface density of charge s and a disc with a density - s. The field at a point M of the axis  according to the principle of superposition is the vector sum of the fields created by each of these distributions taken separately. Either:   Noting the unit vector normal to the plane and oriented to the point M, z the coast of the point M from the center of the circular opening ,we have , using conventional demonstrated results in progress (demonstrate need to know!): Finally : ∎ Back to exercise ∎ See the list of electromagnetism exercises

∎ See the solution Consider a uniformly charged surface plane which is practiced in an empty hole of radius R and fillers. Determine the electrostatic field at a point M of the axis of the hole. We note s the surface density loads.   ∎ See the solution   ∎ See the list of electromagnetism corrected exercises

∎ Back to exercise   1. Field . Being a point M belonging to the Ox axis. The planes passing through this axis are planes of symmetry of the charge distribution, the direction of the electrostatic field is contained in all these plans: the direction of the field is carried by the axis Ox. On the other hand, the distribution is invariant for all translation parallel to the plane yOz. Therefore : The yOz plan is also a plane of symmetry of the charge distribution. Then E x (- x) = - E x (x). To determine the electric field, we apply the Gauss theorem considering as Gaussian surface  a cylinder of height 2x, with axis Ox and O its center . 2. Speed A charge q of the same charge of the layer is initially blocked by the layer to the point of abscissa x = 0. To cross this layer it is sufficient that the charge q reaches the plane yOz since beyond this level, it is pushed to the right. Applying the theorem of k...

►The solution A particle of charge q> 0 and  mass m   , arrives at x = - a with velocity v o perpendicular to an infinite plane layer ,  of thickness 2a and volume load r> 0 uniform. 1. To determine the characteristics of the electrostatic field vector inside the charged layer. 2. Determine the condition relating to v o to the load passes through the layer. ►See the solution   ►Voir list electromagnetism exercises  

∎ Back to exercise 1. Field Management. The planes containing the point M, perpendicular and orthogonal to the axis of the load distribution are symmetry of this distribution plans: the electrostatic field must therefore have its direction carried by the intersection of these two planes. The field is carried by the radial vector of the cylindro-polar base. 2. Invariances. The distribution is cylindrically symmetric, it is therefore invariance by translation parallel to the cylinder axis and rotating around this axis. 3. Vector electrostatic field. Symmetries and invariances used to write the electrostatic field vector in the form: It shall, in both cases, for Gauss surface a closed cylinder whose axis mingled with  the distribution ,of height h, and radius r. As the field vector and the vector ds t so the radial component of the field is constant along the side surface of the cylinder can be written: ...

∎ See the solution consider a cylinder of radius R and of infinite length, uniformly loaded by volume with a volume density r> 0. 1. What is the direction of the electrostatic field at any point M of space? 2. Show that the value of the electrostatic field depends only on the distance r between M and the cylinder axis. 3. Using the Gauss theorem and specifying the used area, calculate the field in either case: r> R r <R We will give E as a function of r. 4. Calculate the electric potential inside and outside of the cylinder. We impose the condition V = 0 for r = 0. 5. The volume density ρ of the load cylinder is no longer uniform but with cylindrical symmetry (ρ is a function of r).   we give ρ= ρ o (r/R) for r <R and ρ o constant. Determine the electrostatic field in the case where r <R.   ∎ See the solution ∎ See the list of electromagnetism exercises

∎ Back to the exercise Hydrogen atom. 1. electrostatic field. As the vector electrostatic field is opposite the gradient of the potential V and it depends only on r (the distribution having spherically symmetrical) are obtained: 2. Feed field. The flow of the electrostatic field is defined by: As the field's radial component and constant over a sphere of radius r: The study gives limits: to r tends to 0 Φ = 0   for r approaching infinity. According to Gauss, a domestic load sphere of radius r expressed as: . We can therefore conclude that the total charge distribution is zero and that at point O we have a positive point charge q. 3. Volumetric charge density. The charge contained between the spheres with center O and radius r and r + d r is: Is then obtained: This charge density is negative and has a total charge...