Solution : Hydrogen atom - Corrected Exericises on Gauss - electromagnetism



Hydrogen atom.

1. electrostatic field.
As the vector electrostatic field is opposite the gradient of the potential V and it depends only on r (the distribution having spherically symmetrical) are obtained:
2. Feed field.
The flow of the electrostatic field is defined by:
As the field's radial component and constant over a sphere of radius r:

The study gives limits:
to r tends to 0
Φ = 0  for r approaching infinity.
According to Gauss, a domestic load sphere of radius r expressed as:
.
We can therefore conclude that the total charge distribution is zero and that at point O we have a positive point charge q.

3. Volumetric charge density.
The charge contained between the spheres with center O and radius r and r + d r is:

Is then obtained:

This charge density is negative and has a total charge - q.

4. Function
The Studied function is the radial charge density and passes through an extremum at r = a.

5. Hydrogen.
The distance a is the Bohr radius which is the distance to the kernel for which the probability of presence of the electron is maximum.
 
∎ Back to the exercise
∎ See the list of electromagnetism exercises
  

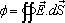
Comments

Post a Comment

Popular posts from this blog

INVASION OF THE SKY - MACHINES

Image
FROM the day when man began to assert his superiority over other animals he began to cast longing eyes at the sky. Fired with ambition and stirred with a spirit of mastery he chafed at the bonds that bound him to earth; but the heavens remained a forbidden kingdom to him. Many a bold adventurer who dared to emulate the birds paid the penalty of his temerity with a broken limb and even with his life. It seemed as if man were destined forever to grovel on the bed of the atmospheric ocean with never a chance to rise except in dreams and fancy. It was not until near the close of the eighteenth century that a means of rising off the earth was discovered. Two brothers, Stephen and Joseph Montgolfier, of Annonay, France, were sitting before a fire, watching the smoke curl up the chimney, when it occurred to one of them that smoke might serve as a vehicle to carry them up into the air. They belonged to a prominent paper-manufacturing family and naturally turned to that materia...
Read more

TRADITIONAL INDUSTRIAL ARTS DESIGN - PRACTICAL METHODS FOR STUDENTS, TEACHERS, AND CRAFTSMEN - BY WILLIAM H. VARNUM 1916

Image
CONTENTS CHAPTER PAGE I. Divisions of Industrial Arts Design 7 II. The Primary Mass and Its Proportions 13 III. Horizontal Major Divisions of the Primary Mass 19 IV. Vertical Major Divisions of the Primary Mass 33 V. Appendages and the Rules Governing Them 43 VI. Enrichment of the Contours or Outlines of Designs in Wood 57 VII. Enrichment of the Contours or Outlines of Designs in Clay 77 VIII. Enrichment of the Contours or Outlines of Designs in Base and Precious Metals 87 IX. Surface Enrichment of Small Primary Masses in Wood 99 X. Surface Enrichment of Small Primary Masses in Wood. (Continued) 117 XI. Surface Enrichment with Minor Subdivisions of Lar...
Read more