Light - Course Of Physics

Course Of Physics

Chapter I. Introduction And Measurement. Page
Chapter II. Molecular Forces And Motions.
Chapter III. Mechanics or Liquids.
Chapter IV. Mechanics Of Gases.
Chapter V. Force And Motion.
Chapter VI. Work And Energy.
Chapter VII. Heat, Its Production And Transmission.
Chapter VIII. Heat And Work.
Chapter IX. Magnetism.
Chapter XI. Static Electricity.
Chapter XI. Electric Currents Produced By VoltaicCells.
Chapter XII. Magnetic Effects Of Electric Currents,And Electrical Measurements.
Chapter XIII. Chemical And Heat Effects Of ElectricCurrents.
Chapter XIV. Induced Currents.
Chapter XV. Sound.
Chapter XVI. Light.

Chapter XVII. Invisible Radiations.
Chapter XVIII. Wireless Telephony And AlternatingCurrents.

352. A Comparison of Sound and Light.?Light from the standpoint of physics is considered much as is sound, as a mode of motion; one affecting the ear, the other producing the result called vision. There are other differences also worth considering. (a) While sound travels as vibrations of some material medium, light travels only as vibrations of the ether; solids, liquids, and gases act so as to hinder rather than to assist in its movement. That is, light travels best in a vacuum or in a space devoid of ordinary matter. (b) The speed of light is so great that at ordinary distances on the earth its motion is practically instantaneous. Experiments have shown that its speed is about 186,000 miles to 300,000 kilometers a second.
353. Luminous and Illuminated Bodies.?If we consider the objects within a room, some of them, as books and furniture, would be invisible if all light from external sources were excluded. On the other hand, some other objects, such as a lighted lamp, a burning coal, or a red hot iron, would be seen if no outside light were present. Such bodies are said to be luminous. Most luminous bodies are hot and become non-luminous on cooling. There are, however, some bodies that are luminous at ordinary room temperatures, as the firefly and some phosphorescent paints. When light emitted by a luminous body strikes an object, a portion of it is always reflected.[Pg 389] It is this reflected light that makes the illuminated object visible. If the object is a sheet of glass, some of the light is transmitted. If a substance is so clear that objects can be seen through it, the substance is transparent, but if objects cannot be seen through it, the substance is said to be translucent. Objects transmitting no light are opaque. Some of the light falling upon a body is neither reflected nor transmitted, but is absorbed and tends to warm the body. The light falling upon a body is therefore either reflected, transmitted, or absorbed. Thus Fig. 345 represents light coming from S to a piece of glass GL. A portion of the light represented by R is reflected. Another part A is absorbed and disappears, while still another part T is transmitted and passes on.

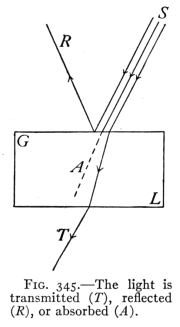Fig. 345.?The light is transmitted (T), reflected (R), or absorbed (A).

There is no sharply drawn line between transparent and opaque bodies. Very thin sheets of gold transmit a greenish light, and experiments have shown that substances as transparent as clear water absorb enough light so that at considerable depths in an ocean or lake little or no light is ever found. All light whether from luminous bodies or reflected from non-luminous objects shows certain properties which will now be considered.
354. The Rectilinear Propagation of Light.?If a beam of light passes through a hole in a window shade into a darkened room, it is seen to follow a perfectly straight course. If a person while coughing holds a book before the face, the sound passes around the book and is heard[Pg 390] at any point in the room while the face is hidden by the book. In other words, light ordinarily does not pass around corners as sound does, but travels in straight lines. This fact is made use of when one aims a gun or merely looks at an object. So well established in our minds is the idea that an object is in the direction from which we see the light coming to us from it, that we are sometimes deceived as to the real position of an object, when the course of the light from it has been changed by a mirror or some other reflecting surface. Many illusions are produced in this way, of which the mirage of the desert is one example. (See Art. 381.)

Fig. 346.?Shadow from a small source of light.

Fig. 347.?Shadow when source of light is large.

355. Shadows.?A shadow is the space from which light is cut off by an opaque body. Thus if a book (see Fig. 346) is held between a screen, N, and a small source of light, L, a shadow is produced which extends from the book to the screen. Notice that the shadow is a space and not an area. If a large gas flame (see Fig. 347) is used as the source of light, the shadow of the book is no longer clear[Pg 391] cut at the edges as before, but has a darker central part with a lighter fringe of partial shadow at the edges. The dark portion within the shadow has all the light excluded from it and is called the umbra. The lighter portion of the shadow at the edges has only a part of the light from the flame cut off. This portion is called the penumbra. when one stands in sunlight his shadow extends from his body to the ground or object on which the shadow falls. At night we are in the earth's shadow, which extends out into space beyond the earth.

Fig. 348.?Character of the earth's shadow.

356. Eclipses.?Since the sun is a very large object the shadow cast by the earth contains both umbra and penumbra. (See Fig. 348.) When the moon passes into the shadow of the earth, there is said to be an eclipse of the moon, while if the moon's shadow falls upon the earth, the portion of the earth cut off from the sun's light has an eclipse of the sun.
357. Images by Small Apertures.?The straight line movement of light makes possible the pin-hole camera, by which satisfactory photographs have been made. The action of this device may be illustrated by placing a luminous body, a lighted candle, an incandescent lamp, or a gas flame, in front of a piece of cardboard, S, which has a small opening in it. Light from the object (see Fig. 349) falls upon a screen, S₂, so as to produce an inverted image. Other applications of this principle will be given later.
[Pg 392]

In Fig. 349 let PQ represent a gas flame, then light from point P at the top of the flame will pass in a straight line through the opening or aperture of the cardboard and strike at P₂ at the bottom of the illuminated spot upon the screen. Light from Q passing in straight lines through the aperture will strike at Q₂ at the top of the lighted space. This spot of light will have the same outlines as the luminous body PQ and being formed as just described will be inverted.

Fig. 349.?Image formed by a small aperture is inverted.

This spot of light, resembling in its outlines the flame, is called an image. An image is defined as an optical counterpart of an object. Images are formed in a variety of devices, such as apertures, mirrors, and lenses. The pin-hole camera is simply a light-tight box with a small aperture in one side. Light passing through this aperture forms an image upon the opposite side of the interior of the box, of whatever object is in front of the camera. Light entering a room through a large aperture such as a window produces a multitude of overlapping images which blend to form a somewhat evenly illuminated surface.

Important Topics

1. Light contrasted with sound (three differences).
2. Bodies: transparent, translucent, opaque.
3. Light: reflected, transmitted, absorbed.
[Pg 393]
4. Light travels in straight lines, evidence, shadows, umbra, penumbra.
5. Formation of images by small apertures.

Exercises

1. Consider the circumference of the earth as 25,000 miles. How many times would the speed of light cover this distance in a second?
2. How soon after any great disturbance takes place on the sun, 93,000,000 miles distant, can it be seen upon the earth?
3. Construct a diagram of the moon's shadow. How much of the sun can one see when in the moon's umbra? When in its penumbra? Have you ever been in either? When? Have you ever been in the earth's umbra? In its penumbra?
4. Explain, using a diagram, the formation of an inverted image by a small aperture.
5. If the sun is 45 degrees above the horizon, what is the height of a pole casting a shadow 60 ft. long?
6. If a shadow 6 ft. long is cast by a 10-ft. pole standing vertically upon a walk, how tall is the tree whose shadow is 42 ft. long, both measurements being made at the same time?
7. Why are the shadows caused by an electric arc lamp so sharply defined?
8. Why should schoolroom windows be all on one side and reach to the ceiling?
9. What is the relation between the size of an image and its distance from the aperture forming it? Can you prove this by geometry?
10. What are silhouettes and how are they produced?

(2) Photometry and the Law of Reflection

358. Photometry.?It is desirable at times to compare the intensities of illumination produced by light from different sources. This is done to determine the relative cost or effectiveness of various illuminants such as candles, kerosene and gas lamps, and electric lights The process of determining the relative intensity of lights or lamps is called photometry. (Photos = light.)
[Pg 394]
The unit for measuring the power of light is called a candle power. It is the light produced by a sperm candle burning 120 grains per hour. An ordinary gas light burns 5 or more cubic feet of gas per hour and yields from 15 to 25 candle power. A Welsbach gas lamp, consuming 3 cu. ft. per hour, produces 50 to 100 candle power.
Instead of using candles, for practical photometry, incandescent lamps standardized by the Bureau of Standards are used for testing or calibration purposes.
It is necessary to distinguish between the intensity of a luminous body, i.e., as a source of light, and the intensity of illumination upon some surface produced by a light. It is considered that two sources of light are of equal intensity if they produce equal illumination at equal distances.
359. Law of Intensity of Light.?A device for measuring the candle power of a light is called a photometer. Its use is based upon the law of intensity of light. The intensity of illumination of a surface is inversely proportional to the square of its distance from the source of light. This relation is similar to that existing between the intensity of a sound and the distance from its source. The following device illustrates the truth of this law in a simple manner.

Fig. 350.?The light spreads over four times the area at twice the distance.

Cut a hole 1 in. square in a large sheet of cardboard (K) and place the card in an upright position 1 meter from an arc light or other point source of light (L). Now rule inch squares upon another card (M) and place it parallel to the first card and 2 meters from it. (See Fig. 350.) The light that passed through the hole of 1 sq. in.[Pg 395] at a distance of 1 meter is spread over 4 sq. in. at a distance of 2 meters. Therefore, the intensity of illumination on each square inch of M is one-fourth that upon the surface of K. If M is placed 3 meters from the light, 9 sq. in. are illuminated, or the intensity is one-ninth that at 1 meter distance.

Fig. 351.?The Bunsen photometer.

These relations show that the intensity of illumination is inversely proportional to the square of the distance from the source of light. An application of the law of intensity is made in using a simple (Bunsen) photometer. This consists of a card containing a spot soaked with oil or melted wax. (See Fig. 351.) The lights whose intensities are to be compared are placed upon opposite sides of the card. The card is then adjusted so that the spot appears the same on both sides. The illumination is now equal on both sides of the card and the candle powers of the two lights are proportional to the squares of their distances from the card. The simple device just described will give approximate results only. For accurate results more elaborate apparatus is required.
360. Measurement of the Intensity of Illumination.?A standard candle (Art. 358) produces when lighted 1 candle power. The illumination caused by this upon a surface 1 ft. away and at right angles to the light rays[Pg 396] is called a foot-candle. It is the unit of intensity of illumination. A 4-candle-power lamp, at a distance of 1 ft., produces 4 foot-candles. A 16-candle-power lamp at a distance of 2 ft. also produces 4 foot-candles?(16 ? 2²).
The intensity of illumination required for a good light for seeing varies with the conditions. Thus, for stage and store lighting about 4 foot-candles are needed, while homes and churches may require but 1 foot-candle.
Too great an intensity of illumination is as harmful as not enough. Exposed lights having an intensity of more than 5 candle power per square inch are often a cause of eye trouble. Such lights should be protected by frosted globes.
A pleasing form of lighting for large halls and public buildings is the indirect system. In this, the lamps are hidden by reflectors which throw the light upon the ceiling from which it is diffused over the room. This form of lighting is more expensive than other systems since but a part of the light is reflected. Its cost therefore is an important factor when considering its use.
361. The Reflection of Light.?The light reflected from the surfaces of bodies about us gives us information concerning our surroundings. A knowledge of the behavior of light undergoing reflection is not usually gained from ordinary observation. The law of reflection of light may be shown, however, by an experiment.

Fig. 352.?B? is as far back of the mirror as B is in front of it.

Christian Huygens

(Popular Science Monthly)
Christian Huygens (1629-1695). Dutch physicist; invented the pendulum clock (1656); developed the wave theory of light; discovered polarization of light (1690).

H. V. Helmholtz

"By Permission of the Berlin Photographic Co., New York."
Hermann von Helmholtz (1821-1894) Germany. Established the doctrine of conservation of energy; made many discoveries in sound; invented the ophthalmoscope; established the physical basis of tone quality.

[Pg 397]
[Pg 398]
[Pg 399]

A plane mirror, M, is held in a vertical position resting upon a sheet of paper. (See Fig. 352.) Pins are set upright in the paper at A and B. On placing the eye along the line AC and looking toward the mirror an image of B may be seen in the mirror due to the light reflected from its surface. Pins C and D are now set in the paper so that when one looks along the line BD toward the mirror one may see all four pins apparently in one line. This indicates that the light from A and C passing along CA toward O is reflected back along the light CBD. By means of a ruler, draw lines through BD and AC till they intersect at O. Also draw PO perpendicular to the mirror at O.

Then the angles AOP and BOP will be found equal. These are called the angles of incidence and reflection respectively. The law of reflection is therefore stated: The angle of reflection is equal to the angle of incidence. These angles are in the same plane, that of the paper. This law applies in all cases of reflection of light. It is similar to the law of reflection of sound (Art. 326.)

Important Topics

1. Photometry, law of intensity, candle power, foot-candle.
2. Intensity of illumination.
3. Reflected light and law of reflection.

Exercises

1. Both sides of a card are equally illuminated when two lights are on opposite sides of it and 10 and 30 cm. respectively from it. what are their relative intensities?
2. What are the relative intensities of illumination from a gas light upon a book 6 ft. and 2 ft. respectively from the light?
3. Which is more expensive per candle power? How many times as expensive? A 50-watt 16-candle-power incandescent lamp at 10 cents per kilowatt-hour or a 100-candle-power Welsbach light burning 5 cu. ft. of gas per hour at 80 cents per 1000 cu. ft. of gas. (Find cost of each per hour, and then the cost of 1 candle power hour for each.)
4. Why are not ordinary shadows perfectly dark?
5. At what distance will a 16-candle-power lamp give the same illumination as a single candle at 10 in.?
6. If the sun is at an elevation of 30 degrees what is the angle of incidence at which it strikes the surface of water? What is the angle between the incident and the reflected rays?
[Pg 400]
7. What is the difference between the phenomena of reflection of light from a white sheet of writing paper and from a piece of clear window glass?
8. A horizontal ray of light, traveling due east, strikes a vertical mirror so that after reflection it is traveling due north. If the mirror be now turned 10 degrees about a vertical axis, the north edge moving east, what will be the direction of the reflected ray?
9. The necessary illumination for reading is about 2 foot-candles. How far away may an 8-candle-power lamp be placed?
10. What is the illumination in foot-candles upon a surface 20 ft. from an arc lamp having an intensity of 1000 candle power?
11. How far from a 100-candle-power Welsbach light would the illumination be 2 foot-candles?

(3) Mirrors and the Formation of Images

Fig. 353.?Reflection of light, (a) diffused, (b) regular.

362. Mirrors.?The many purposes served by mirrors in our every-day life has made their use familiar to everyone. Yet without study and experiment few understand their properties and action. Any smooth surface may serve as a mirror, as that of glass, water, polished wood, or metal. Most objects, unlike mirrors, have irregular surfaces; these scatter or diffuse the light that falls upon them. (See Fig. 353a.) This is called diffused or irregular reflection. The reflection of light from the smooth surface of a mirror is regular. (See Fig. 353b.) In every case of reflected light, however, the angle of reflection equals the angle of incidence, diffusion being due to the irregularity[Pg 401] of the surface. It is by means of the light "diffused" from the surface of illuminated bodies, such as plants, animals, food, and manufactured articles, that we "see" the various objects about us, and it is this light that enables us to judge of their distance, size, form, color, etc. The moon is seen by the sunlight reflected from its surface. Moonlight is therefore sunlight diffused by reflection. The new moon is that phase or condition of the moon when only a narrow strip of the moon's illuminated surface is turned toward the earth. At the time of the full moon the whole illuminated surface is seen.
363. Images Formed by a Plane Mirror.?The most common use of mirrors is in the formation of images. The way in which images are formed by a plane mirror may be illustrated by diagrams. Thus in Fig. 354, let L represent a luminous body and E and E? two positions of the observer's eye. Take any line or ray as LO along which the light from L strikes the mirror O-O?. It will be reflected so that angle LOP equals angle POE. Similarly with any other ray, as LO?, the reflected ray O?E? has a direction such as that angle L?O?E? equals angle P?O?E?. Any other rays will be reflected in a similar manner, each of the reflected rays appearing to the eye to come from a point L? behind the mirror.

Fig. 354.?The virtual image of a fixed object as seen in a plane mirror, has the same location from every position of the observer's eye.

364. Light Waves and Wave Diagrams.?Just as a stick continually moved at the surface of a body of water sets up a series of waves spreading in all directions, so one may imagine a train of waves sent out by a luminous[Pg 402] body L (as in Fig. 355) to the mirror MN. These waves will be reflected from the mirror as if the source of light were at L?. It is much simpler and more convenient to locate the position of the image of a point by the use of lines or "rays" (as in Fig. 354) than by the wave diagram (as in Fig. 355). In all ray diagrams, however, it should be kept in mind that the so-called ray is a symbol used to represent the direction taken by a part of a light wave. Thus in Fig. 354, the light from L moving toward O is reflected to E along the line OE, the heavy lines representing rays.

Fig. 355.?Wave diagram of image formed in a plane mirror.

365. To locate the image of an object formed by a plane mirror requires simply an application of the law of reflection. Thus in Fig. 356 let AB represent an object and MN a plane mirror. Let AA? be a ray from A striking the mirror perpendicularly. It is therefore reflected back along the same line toward A. Let AO represent any other ray from A. It will be reflected along OE so that angle r equals i. The intersection of AC and OE at A? behind the mirror locates the image of the point A, as seen by reflection from the mirror. The triangles ACO and A?CO may be proved equal by geometry. Therefore[Pg 403] A?C equals AC. This indicates that the image of a point formed by a plane mirror is the same distance back of the mirror as the point itself is in front of it. This principle may be used in locating the image of point B at B?. Locating the position of the end points of an image determines the position of the whole image as A?B?.

Fig. 356.?The image A?B? is as far back of the mirror M N as the object A B is in front of the mirror.

366. How the Image is Seen.?Suppose the eye to be placed at E. It will receive light from A by reflection as if it came from A?. Similarly light starting from B reaches the eye from the direction of B?. There is nothing back of the mirror in reality that affects our sight, the light traveling only in the space in front of the mirror. Yet the action of the reflected light is such that it produces the same effect as if it came from behind the mirror. Images such as are seen in plane mirrors are called virtual to distinguish them from real images, in which light actually comes to the eye from the various parts of the visible image, as from the real image formed by a projecting lantern upon a screen, or by an aperture as in the pin-hole[Pg 404] camera. Real images therefore are those that can be obtained upon a screen while virtual images cannot.
367. Multiple Reflection.?If the light from an object is reflected by two or more mirrors various effects may be produced, as may be illustrated by the kaleidoscope. This consists of three plane mirrors so arranged that a cross-section of the three forms an equilateral triangle. The mirrors are placed in a tube across the end of which is a compartment with a translucent cover containing pieces of colored glass. On looking through the tube, the reflections from the several surfaces produce beautiful hexagonal designs.

Fig. 357.?Perspective view of "Pepper's ghost."
Fig. 358.?Diagram of the "Pepper Ghost" illusion.

368. Optical Illusions by a Plane Mirror.?The illusion called Pepper's Ghost is typical of many illusions produced by reflection. It may be illustrated by taking a piece of plate glass, M-N, a tumbler of water, W, and a lighted candle, C, placed in a box, B, having one side open and arranged as shown in perspective in Fig. 357, and in section in Fig. 358. If the effect is produced in a darkened room, the observer at E sees a virtual image of the lighted candle as if it were in the glass of water, the water being seen by transmitted light through the plate glass, the[Pg 405] latter forming a virtual image of the candle by reflection. Some of the illusions produced by this means are: (a) the figure suspended in mid air; (b) the bust of a person without a trunk; (c) the stage ghost; (d) the disappearing bouquet.

Fig. 359.?Action of a concave mirror on parallel rays of light.

Fig. 360.?Real image formed by a concave mirror.

369. Concave Mirrors.?Another useful piece of physical apparatus is the concave spherical mirror. It is frequently made from plano-convex lenses by silvering the convex surface of the lens, thus making a concave reflecting surface from the inner surface of the silvered part; they are also made by polishing the inner surfaces of metallic spherical shells. The concave mirror is represented in section in Fig. 359 by the curve MN; C is the center of curvature or the center of the surface of which this mirror MN is a part; the line VC through the center V of the mirror is called the principal axis; while any other line passing through C is called a secondary axis. The point midway between the vertex V and center of curvature C is called the principal focus, F. It is the point through which parallel incident rays pass after reflection. The angle MCN which the curve of the mirror subtends at the center is called the aperture of the mirror. We learned in Art. 361, the angle of reflection of a ray of light is always equal to the angle of incidence no matter what the nature of the reflecting surface may be. If the reflecting surface[Pg 406] is a regular concave surface, like the inner surface of a sphere, the rays of light coming from a point source may after reflection come to a focus, forming a real image. The two extreme points of an object should be selected for locating its image; Fig. 360 shows the construction. The real images formed by concave mirrors are always inverted. The principal focus of a concave mirror may be observed by holding the mirror in a beam of sunlight entering a darkened room. The sun's rays after reflection converge to form a small, round, intense spot of light, which is a real image of the sun, located at the principal focus of the mirror. The distance of the principal focus from the mirror is the least distance that a real image can be formed in front of a concave mirror.
370. Virtual Images by Concave Mirrors.?When light comes from a small point situated between a concave mirror and its principal focus, the reflected rays are divergent and hence no real image of the object can be found in front of the mirror. But if the rays are extended behind the mirror they will meet in a point called the virtual focus. This is the point from which they appear to come. Any image of an object situated between the principal focus and a concave mirror is therefore a virtual image, erect and larger than the object. (See Fig. 361.)

Fig. 361.?Virtual image formed by a concave mirror.

371. Construction of Real Images.?There are five positions at which an object may be situated in front of a concave mirror, namely: (1) beyond C; (2) at C; (3) between C and F; (4) at F and (5) between F and V. There are two ways by means of which the image formed at each[Pg 407] of these positions may be located, namely; (1) experimentally, by allowing the rays of light from a luminous body to focus on a screen and (2) diagrammatically. By the latter method the two rays of light are considered the course of each of which may easily be determined; first, the ray which strikes the mirror parallel to its principal axis and which after reflection passes through the principal focus; second, the ray which passing through the center of curvature strikes the mirror at right angles and therefore after reflection must pass directly back along its incident path. Where these two reflected rays intersect is located the real image of the object. Whenever these two rays of light do actually intersect, as in Fig. 360, a real image (ab) is formed of the object AB.
The points A and a, B and b and others similarly situated on an axis extending through the center of curvature C are called conjugate foci, for they are so related that an object being at either one, its image will be found at the other.

Fig. 362.?Action of a convex mirror upon parallel rays of light.

372. The Convex Mirror.?There are few practical uses to which convex mirrors can be put. They are sometimes used to give the chauffeur of an automobile a view of the road behind him. It is then attached to the wind shield by a short rod. The reflected rays coming from a Convex mirror are always divergent (see Fig. 362), hence the image is always virtual and located behind the reflecting surface. The method of construction for images formed by a convex mirror is similar to that for concave mirrors. (See Fig. 363.) The center of curvature and principal focus are behind[Pg 408] the mirror and consequently the reflected rays have to be produced backward until they meet. The images are always virtual, erect and smaller than the object.

Fig. 363.?Construction of an image by a convex mirror.

Fig 364.?Illustrations of Spherical Aberration.

373. Spherical Aberration. Sometimes in a concave mirror when the aperture MCN (Fig. 364) is large the images are blurred or indistinct. This is due to the fact that the incident rays near the outer edge of the mirror do not focus after reflection at the same point as those which pass into the mirror near the vertex, but cross the principal axis at points between the mirror and principal focus as is shown in Fig. 364; this result is called spherical aberration. The larger the aperture of the mirror the more the image is blurred. Concave mirrors in practical use do not have an aperture much greater than 10 degrees. This non-focusing of the rays of light by curved reflecting surfaces may be noticed in many places, as when light is reflected from the inside of a cup that contains milk or from the inside of a wide gold ring placed on top of a piece of white paper. The pupil will note other[Pg 409] instances. This curve of light observed is called the caustic by reflection.
374. Parabolic Mirrors.?The best possible surface to give to concave mirrors is parabolic. This is a curve which may be generated by moving a point so that its distance from a fixed point and a fixed line are always equal. If a source of light is placed at F the rays after reflection are rendered parallel. See Fig. 365. This reflector is used in automobile lamps, headlights of locomotives, search-lights, etc. It is also used in large reflecting astronomical telescopes to collect as large an amount of light as possible from distant stars and bring it to a focus. Such mirrors may be made exceedingly accurate.

Fig. 365.?Parabolic mirror.

Important Topics

1. Reflection: regular, diffused; plane mirrors; laws of reflection.
2. Formation and location of images by plane mirrors. Wave and ray diagrams.
3. Multiple reflection, illusions.
4. Curved mirrors, uses; concave, convex, parabolic.

Exercises

1. Distinguish between regular and diffused reflection. By means of which do we see non-luminous bodies?
2. Could a perfect reflecting surface be seen? Explain.
3. A pencil is stood upright in front of a plane mirror set at an angle of 45 degrees to the vertical. Shown by a diagram the location and position of the image.
4. Show by diagrams the position and location of the images of a pencil (a) when standing erect and in front of a vertical mirror. (b) when standing upon a horizontal mirror.
5. What is the difference between a real and a virtual image?
[Pg 410]
6. A standard candle and a lamp give equal illuminations to a screen that is 1 ft. from the candle and 6 ft. from the lamp. What is the candle power of the lamp? Explain.
7. Why are walls finished in rough plaster or painted with soft tones without gloss better for schoolrooms than glossy paints or smooth white plaster?
8. Try to read a printed page by looking at its image in a mirror. write your name backward on a sheet of paper, and then look at the image of the writing in a mirror. What effect is produced by the mirror in each case?
9. If the point of a pencil is held to the surface of a piece of plate-glass mirror two or more images may be seen in the mirror. Explain.
10. Given a small lighted candle, a concave mirror, a meter stick, and a white screen, how would you prove the statements made in Arts. 369 and 370 concerning the location of images formed by concave mirrors? Make the diagram in each case.
11. Why do images seen in a quiet pond of water appear inverted? Explain by a diagram.

(4) Refraction of Light

375. Common Examples of Refraction.?Everyone has noticed the apparent bending of an oar, of a stick, or of a spoon when placed in water (see Fig. 366), while many have observed that the bottom of a pond or stream looks nearer to the surface than it really is. These and similar illusions are due to the refraction or bending of light rays as they pass from one medium to another. The principles of refraction are among the most useful found in the study of light since application is made of them in the construction and use of important optical instruments, such as the camera, microscope, telescope, and the eye.

Fig. 366.?The stick appears to be bent on account of refraction.

[Pg 411]
376. Action of Light Undergoing Refraction.?If a beam of sunlight be admitted to a darkened room and reflected by a mirror so that it strikes the surface of water in a glass jar, a part of the beam may be seen to be reflected while another portion is transmitted through the water (Fig. 367). The reflected beam follows the law of reflection while the transmitted beam is seen to be refracted, or to have its courses slightly changed in direction upon entering the water. If the mirror is turned so that the angle at which the light strikes the water is changed, the amount of refraction or change of course of the light is varied. When the light strikes the water perpendicularly there is no refraction. On the other hand, the greater the angle at which the light strikes the water the greater the bending.

Fig. 367.?Part of the ray is reflected and part passes into the water and is refracted.

Fig. 368.?Illustrating the laws of refraction of light.

377. Laws of Refraction. The action of light on entering, passing through, and leaving a great variety of substances has been carefully studied. A summary of the results of these observations is given in the following laws of refraction: I. When light enters a transparent body, perpendicularly, it passes on without changing its direction.[Pg 412] II. When light enters a denser transparent body obliquely, it is bent toward the perpendicular; when light enters a less dense body obliquely, it is bent away from the perpendicular. (See Fig. 368.)
378. The cause of refraction may be illustrated by considering a line of men moving across a field and occupying at equal time intervals the successive positions 1, 2, 3, etc., indicated in Fig. 369. Suppose that the upper and lower parts of the field have a smooth hard surface, while at the center is a strip of newly ploughed ground. The line will move more slowly over the ploughed field than over the hard field. This will result in a retardation of the end of the line first striking the soft ground with a resulting change of direction of the line, toward the perpendicular to the edge of the field (on entering the place of more difficult travel), and away from the perpendicular on moving into a place where increased speed results.

Fig. 369.?Diagram illustrating the cause of refraction.

379. Index of Refraction.?By studying the change of direction of the marching men as shown in Fig. 369 it is evident first that it is due to a difference in speed in the two media. It is not easy to measure the speed of light in a medium. However, the amount of refraction may be determined easily and from this the relative speed may be computed. The number that expresses the ratio of the speed of light in air to its speed in another medium is called the index of refraction of that medium. The relative speeds of light, or the indices of refraction for some substances, are:[Pg 413] water, 1.33, crown glass, 1.51, flint glass, 1.61, diamond, 2.47, carbon bisulphide, 1.64.

Fig. 370.?The incident ray and the emergent rays are parallel.

380. Plates, Prisms, Lenses.?The refraction of light is usually observed when it is passing through a plate, a prism, or a lens. The important differences between the effects of each in refracting light are illustrated in Figs. 370, 371 and 372. In Fig. 370 it is seen that the refraction of the ray on entering the glass is counteracted by the refraction away from the perpendicular upon leaving it. So that the entering and emergent rays are parallel. In Fig. 371 the refraction at the two surfaces of the prism results in a change of direction of the ray, the course being bent toward the thicker part of the prism. In Fig. 372 it may be noticed that the convex lens resembles two prisms with their bases together. Since all parts of the lens refract light toward the thicker part, the center, the effect of the convex lens is to bring the rays of light to a focus, at F.

Fig. 371.?Effect of a prism upon a ray of light.
Fig. 372.?The convex lens brings the rays of light to a focus.

381. Total Reflection.?It has been shown that when light passes from a denser to a lighter medium, as from glass[Pg 414] or water to air, that the beam is refracted away from the perpendicular. This is illustrated in Fig. 373. The diagram represents the change in the course of a ray of light that passes through water to a surface with air above it. A ray striking perpendicularly passes through without refraction. Other rays show increasing refraction with increasing angle of incidence. For one ray the angle of refraction is so large that the refracted ray is parallel to the surface. When this condition is reached, the angle of incidence is called the critical angle. Any increase in the angle of incidence causes all of the light to be reflected as is the beam E. This action is called total reflection, the course of the reflected ray being according to the law of reflection. A right-angle prism (see Fig. 374) is often used where a mirror would ordinarily be employed, the total reflection occurring within the prism giving more satisfactory results than a mirror. See Art. 398 for a description of the Zeiss binocular field-glass for an example of this use of total reflection.

Fig. 373.?An example of total reflection.
Fig. 374.?Total reflection in a right-angle prism.

The mirage (see Fig. 375) is an optical illusion by which distant objects, below the horizon, are sometimes plainly seen. This phenomenon is most frequently observed in hot, desert regions, when the air conditions are such that the lower strata near the ground are very much hotter than those above. These lower strata, having expanded the most, are less dense than the cooler ones above. Hence a ray of light traveling obliquely downward is refracted more and more until total reflection takes place. The images seen are inverted[Pg 415] giving a representation of trees or other objects reflected on the surface of still water. The mirage is also frequently seen at sea, ships being observed, sometimes erect, sometimes inverted, apparently sailing in the clouds near the horizon. Over the Great Lakes, trees, boats, and towns on the opposite shore, sixty or seventy miles away, can sometimes be plainly seen, apparently but a few miles out. In this case the images are erect, the total reflection being from warm, still layers of air over colder layers near the water.

Fig. 375.?Diagram of a mirage.

Important Topics

(A) Refraction: cause, illustration, two principles.
(B) Index of refraction, meaning.
(C) Plates, prisms, lenses, action of each.
(D) Total reflection, uses.

Exercises

1. Compute the speed of light in water, the index of refraction being 1.33.
2. If one wished to shoot a fish under water, should he aim at the apparent location of the fish as viewed from the air? Explain, using a diagram.
3. Define refraction. Mention two illustrations of this action that you have observed out of school.
4. Why does the moon look larger near the horizon?
5. Is your reflection seen in a pool of water upside down? Why?
6. Why does it whiten molasses candy to pull it?
7. When looking at a building through the ordinary glass of a window why do straight lines of the building appear to be so distorted? What makes them appear to move as you move your head slightly?
[Pg 416]
8. Explain the phenomenon which one observes when looking at an object through the air arising from a hot stove or radiator.
9. Frequently the horizontal diameter of the setting sun appears to be greater than the vertical. Explain.
10. Explain why one observes several images of a luminous body like a lighted candle when the reflected light from a thick glass mirror enters the eye, the angle of reflection being large.

(5) The Formation of Images by Lenses

382. Uses of Lenses in Optical Instruments.?The use of instruments that employ lenses in their operation, such as spectacles, reading and opera glasses, and the camera, microscope, and telescope, is familiar to most students of physics. The part played by the lenses, however, is not generally understood. Consequently the study of the formation of images by lenses is of general interest and importance.
383. Forms of Lenses.?While a lens may be formed from any transparent solid it is commonly made of glass. It may have two curved surfaces or one curved and one plane surface. Most lenses are spherical lenses, since their curved surfaces form a part of the surface of a sphere. Fig. 376 represents a spherical lens with a curved surface coinciding with that of a sphere whose center is at C. This center is called the center of curvature, while the radius of the sphere R, is the radius of curvature.

Fig. 376.?Formation of a spherical lens.

There are two classes of lenses: those thick in the middle are called convex, while those thick at the edges are concave. The mode of constructing the six forms of spherical lenses is shown in Fig. 377. These are named as follows: (1) double convex, (2) plano convex, (3) concavo-convex, (4) double concave, (5) plano concave, (6) convexo-concave.
[Pg 417]

Fig. 377.?Forms of Lenses. 1. double convex; 2. plano convex; 3. concavo convex; 4. double concave; 5. plano concave; 6. convexo concave.

Fig. 378.?The action of a burning glass.

384. Effect of Lenses upon Light.?The most important characteristic of a lens is its effect upon a beam of light. Most persons have seen a "burning glass," a double convex lens, used to bring to a point, or focus, a beam of sunlight. To show the action of a burning glass send a beam of light into a darkened room, and place in its path a double convex lens. (See Fig. 378.) If two blackboard erasers are struck together near the lens, the chalk particles in the path of the light are strongly illuminated, showing that the light after passing through the lens it brought to a focus and that it spreads out beyond this point. This point to which the cone of light rays converges after passing through the convex lens is called the principal focus of the lens. The distance from the principal focus to the center of the lens is the focal length or principal focal distance of the lens. The focal length of double convex lenses of crown glass is about the same as the radius of curvature of either surface.[Pg 418] The action of a convex or converging lens upon light may be better understood by studying Fig. 379 in which light is passing from S to F. The successive positions and shape of the advancing light waves are indicated by lines drawn across the beam. The light being retarded more in the thicker part of the lens, the light waves on leaving the lens have a concave front. Since light waves tend to move at right angles to the front of the wave, the light is brought to a focus. After passing the focus the waves have a convex front, forming a diverging cone.

Fig. 379.?Wave diagram of light passing through a convex lens.

385. Concave Lenses.?When sunlight passes through a concave lens a diverging cone of light is formed. (See Fig. 380.) This is caused by the edges of the wave being retarded more than the center, producing a convex wave front. This diverging cone of light acts as if it had proceeded from a luminous point at F.
This point is called a virtual focus and is nearly at the center of the curvature of the nearer surface.

Fig. 380.?Wave diagram of light passing through a concave lens.

386. The Formation of Images by Lenses.?If a beam composed of parallel rays of light, as sunlight, is sent in[Pg 419] turn through three convex lenses of the same diameter but of different thickness, it is found that the thicker the lens the greater is its converging power, or the shorter is its focal length. (See Fig. 381.) Now if a luminous body, such as a lighted candle, be placed near the convex lens but beyond its focal length, the light will be brought to a focus upon the other side of the lens and an image of the candle may be clearly seen upon the screen placed at this point. (See Fig. 382.) The two points so situated on opposite sides of a lens that an object at one will form an image at the other are called conjugate foci.

Fig. 381.?The thicker the lens, the shorter is its focal length.

Fig. 382.?C and S are at conjugate foci.

It will be helpful to compare the images formed of a candle by an aperture and by a convex lens. Rays of light from each point of the luminous body pass through[Pg 420] the aperture in straight lines and produce upon the screen a lighted space of the same shape as the candle. This image is rather hazy in outline. Each cone of rays from luminous points of the flame is brought by the lens to a focus on the screen, producing a sharp image. It is the converging power of convex lenses that enables them to produce clear images.

Fig. 383.?Construction of a real image by a convex lens.

387. The Construction of Diagrams to Represent the Formation of Images by Lenses.?Just as the earth has an axis at right angles to its equator to which are referred positions and distances, so a lens has a principal axis at right angles to its greatest diameter and along this axis are certain definite positions as shown in Fig. 383. Let MN be the principal axis of a convex lens, P and P? are principal foci on either side of the lens, S and S? are secondary foci. These are at points on the principal axis that are twice as far from O, the center of the lens, as are the principal foci. In the formation of images by a convex lens, several distinct cases may be noticed:
(A) If a luminous body is at a great distance at the left, its light is brought to a focus at P, or its image is formed at P. (B) As the object approaches the lens the image gradually recedes until the object and image are at S and S?, equally distant from O and of equal size (as in Fig. 383). The object and image are now said to be at the secondary foci of the lens. (C) As the object moves from S to P the image recedes, rapidly increasing in size until (D) when[Pg 421] the object is at P the rays become parallel and no image is formed. (E) When the object is between P and the lens, the rays appear to proceed from points back of the object, thus forming an erect, larger, virtual image of the object. (See Fig. 384.) This last arrangement illustrates the simple microscope.
With a concave lens but one case is possible, that corresponding to the one last mentioned with convex lenses; since the rays from a body are divergent after passing through a concave lens they appear to proceed from points nearer the lens than the object and hence a virtual, erect, smaller image of the object is formed. This virtual image may be seen by looking through the lens toward the object. (See Fig. 385.)

Fig. 384.?Construction of a virtual image by a convex lens.

Fig. 385.?Construction of a virtual image by a concave lens.

388. The Lens Equation.?The location of either the object or of the image upon the principal axis of the lens may be calculated if the position of one of these and the[Pg 422] focal length are known. This is accomplished by the use of a formula 1/F = 1/D₀ + 1/D₁ in which F represents the focal length and D₀ and D₁ the distance from the lens of the object and the image respectively. Thus if an object is placed 30 cm. from a lens of 10 cm. focal length, where will the image be formed? Thus: 1/10 = 1/30 + 1/D and 3D₁ = D₁ + 30, or 2D₁ = 30 D₁ = 15. This result indicates that a real image will be 15 cm. from the lens. A minus value would indicate a virtual image.

Important Topics

(A) Lenses: convex, concave, six forms, center and radius of curvature.
(B) Principal focus, focal length, virtual focus, conjugate foci.
(C) Principal axis, images formed when object is in various locations.
(D) Computation of location of images.

Exercises

1. Why is an image of a candle formed by an aperture, not sharply defined?
2. When a photographer takes your picture and moves the camera nearer you, must he move the ground glass screen toward the lens or away from it? Explain.
3. How can you find the principal focal length of a lens.
4. How can you test a spectacle lens to see whether it is convex concave?
5. When will a convex lens produce a virtual image? Have you ever seen one? Where?
6. When a photographer wishes to obtain a full length view of a person, where does he place the camera?
7. The focal length of the lens is 24 cm. How far from the lens must an object be placed in order that a real image may be three times as long as the object?
8. There is a perfect image of an object on the ground glass of a camera. The center of the lens is 20 cm. in front of the image[Pg 423] and the object 75 cm. from the lens. What is the focal length of the lens?
9. An object is 60 cm. from the lens, the image 120 cm. from it. Find the focal length.
10. How can you find experimentally the principal focal length of a lens?
11. A lens is used to project an enlarged image of a candle upon a screen. Which is farther from the lens, the candle or the image? Explain.

(6) Optical Instruments

389. The Eye.?The most common optical instrument is the eye. While the structure of the eye is complicated, the principle of it is simple, involving the formation of an image by a double convex lens. (See Fig. 386, in which is shown a front to back, vertical cross-section of the eye.) The eye appears to be made of portions of two spheres, one of which, smaller than the other, is placed in front. This projecting part is transparent, but refracts the light which strikes it obliquely, so as to turn it into the eye. This enables us to see objects at the side when looking straight ahead. Test this by looking directly in front of you and see how far back on each side of the head you can notice a movement of the forefinger of each hand.

Fig. 386.?Cross-section of the eye.

390. Action of the Eye in Vision.?When we look at an object, a small, real, inverted image is formed upon the retina at the back of the interior of the eye. The retina is an expansion of the optic nerve and covers the inner surface at the back of the eyeball. Seeing is due to the action of light in forming images upon the retina. Our eyes are so constructed that when they are relaxed the lens is adjusted[Pg 424] to form clear images of distant objects upon the retina. If we look from distant to near objects without changing the shape of the eye lens, a sharp image of the latter cannot be formed and we get a blurred impression. It is difficult, however, to look at objects without automatically adjusting the eye lens so that it will make a sharp image. Test this by looking out of a window at a distant object, then without moving the head or eyes look at the glass of the window; you will notice a slight change of some sort in the eye itself as the vision is adjusted. This adjustment is made by muscles that pull or compress the eye lens so as to make it thicker for near objects and thinner for distant ones. The eye ordinarily does not see objects nearer than 10 in. clearly. This means that the greatest possible thickening of lens will not form clear images upon the retina if the object is nearer than 10 in. (25 cm.).

Fig. 387.?The visual angle, AOB is greater at AB than at A?B?.

391. The Visual Angle.?To examine objects carefully we usually bring them as close to the eye as possible, for the nearer to the eye the object is brought, the larger is the visual angle formed by it (see Fig. 387), and the larger is its image upon the retina. The visual angle of an object is the angle at the eye lens between the rays that have come from the ends of the object. Consequently the more distant the object, the smaller is its visual angle. Now if we wish to examine small objects with great care, we frequently find that it is necessary to bring them close to the eye so that they have a visual angle of adequate size. If they must be brought closer than 10 in. a double convex lens is placed in front of the eye. This assists the eye lens in converging the light so that a clear image may be formed[Pg 425] when the object is close, say an inch or so from the eye. This is the principle of the magnifying glass used by watch-makers and of the simple microscope. The action of the latter is illustrated by Fig. 388. The convex lens forms a virtual, enlarged image "A?-B?" of the object "A-B" which it observed instead of the object itself.

Fig. 388.?Action of the simple microscope.

Fig. 389.?"Near sightedness", or myopia. Parallel rays come to a focus at F; emerging rays focus at A, the far point.

392. Defects of Vision.?There are several defects of vision that may be corrected by spectacles or eye-glasses. One of these is "near-sightedness." It is due either to an eyeball that is elongated, or to an eye lens that is too convex, or to both conditions. This condition brings light from distant objects to a focus too soon (as shown in Fig. 389). Only light from near objects will focus upon the retina in such cases. With normal vision light from distant or near objects may be focused without unusual effort upon the retina, see Fig. 390. The remedy for near-sightedness is to use concave lenses which will assist in properly refracting the light so the focus will be formed on the retina (Fig. 391). "Far-sightedness" is the reverse of near-sightedness; the eyeball is either too short, or the lens too flat, or both conditions obtain, so that the light entering the eye is brought to a focus behind the eyeball (Fig. 392). The remedy is convex lenses which will assist in properly converging the light, see Fig. 393. A[Pg 426] third defect is called astigmatism. This is caused by some irregularity or lack of symmetry in the eye. It is corrected by a cylindrical lens that compensates for this defect of the eye. A diagram similar to Fig. 394 is used as a test for astigmatism. If the lines appear with unequal distinctness, some irregularity of refraction (astigmatism) is indicated.

Fig. 390.?The normal eye. The parallel rays A B focus without accommodative effort at C.
Fig. 391.?Correction of near-sightedness by concave lens.
Fig. 392.?Far-sightedness or hyperopia. Parallel rays focused behind the retina.

Fig. 393.?Correction of far-sightedness by a convex lens.
Fig. 394.?Test card for astigmatism.

393. The Photographic Camera.?This is a light-tight box, provided with a convex lens in front, covering an aperture and a ground glass[Pg 427] screen at the back. The distance between the lens and the screen is adjusted until a sharp image is obtained upon the latter, which is then replaced by a sensitive plate or film. The sensitized surface of the plate or film contains a salt of silver which is changed by the action of light. After the plate has been "exposed" to the action of light, it is "developed" by the use of chemicals producing a negative image. From "negative," by the use of sensitized paper, "positive" prints may be secured which resemble the object photographed.

Fig. 395.?Diagram of the projecting lantern.

394. The projecting lantern (see Fig. 395) employs a strong source of light, as an electric arc lamp L, to strongly illuminate a transparent picture, or lantern slide, S, a real image (I) of which is formed upon a large screen. Two large plano-convex lenses (C), called condensing lenses, are placed near the lamp to concentrate the light upon the "slide" S. The convex lens forming the image is called the "objective" (O).
395. The compound microscope consists of two lenses. One called the objective is placed near the object to be viewed. This lens has a short focal length usually less than a centimeter. It forms a real image of the object. A?-B?. The other lens, the eyepiece forms a virtual image of this real image. A??-B??. (See Fig. 396.)
[Pg 428]
396. The telescope consists of two lenses, the eyepiece and the objective. As in the compound microscope, the objective of the telescope forms a real image of the distant object, the eyepiece forming an enlarged virtual image of the real image. It is the virtual image that is viewed by the observer. (See Fig. 397.) In order to collect sufficient light from distant stars the objective is made large, sometimes 50 in. in diameter.

Fig. 396.?Formation of an image by a microscope. A-B is the object. B?-A? the real image formed by the "objective." B??-A?? is the virtual image formed by the eyepiece. The eye sees the virtual image.

The length of the telescope tube depends upon the focal length of the objective, since the distance between the two lenses must equal the sum of their focal lengths.

Fig. 397.?Formation of an image by a telescope. b-a is the real image; d-c is the virtual image seen by the observer.

397. The opera glass consists of a convex lens as objective and a concave lens as an eyepiece. The former tends to form a real image but the latter diverges the rays before a real image can be formed, the action of the two lenses producing an enlarged virtual image (as in Fig. 398) which[Pg 429] is viewed by the one using the glass. The compact size of the opera glass is due to the fact that the distance between the two lenses is the difference of the focal lengths.

Fig. 398.?Formation of an image by an opera-glass. a-b is the virtual image.

Fig. 399.?Diagram of the Zeiss binocular or prism field glass.

398. The Prism Field Glass or Binocular.?This instrument. has come into use in recent years. It possesses the wide field of view of the spy glass but is as compact as the opera glass. This compact form is secured by causing the light to pass back and forth between two right-angle prisms (as shown in Fig. 399). This device permits the use of an objective lens with a focal length three times that of the tube, securing much greater magnifying power than the short instrument would otherwise possess. A further advantage is secured by the total reflection from[Pg 430][Pg 431] the two prisms, one of which is placed so as to reverse the image right for left and the other inverts it, so that when viewed in the eyepiece it is in its proper position.

Important Topics

1. The eye: parts, formation of image, kind, how, where.
2. Eye defects, how remedied. Visual angle.
3. Simple microscope, camera; images, kind, how formed.
4. Compound microscope, telescope and opera glass; images, action of each lens.

Exercises

1. Name three instruments in which lenses form virtual images and three in which real images are formed.
2. In what direction is an oar in water apparently bent? Explain by a diagram.
3. What optical instruments have you used? Is the visible image formed by each of these real or virtual?
4. The focal length of a copying camera lens is 14 in. Where must a drawing be placed so that an image of the same size may be formed upon the ground glass screen? What must be the distance of the screen from the lens?
5. What are two methods by which you can determine the focal lengths of the lens of a photographic camera?
6. The critical angle for water is 48-1/2 degrees. Show by a diagram how much of the sky can be seen by a diver who looks upward through the water.
7. How is near-sightedness caused? How is it corrected? Illustrate by a diagram.
8. How is the eye accommodated (focused) as an object gradually approaches it?
9. Explain why a simple microscope assists in looking at the parts of a flower or insect.
10. Why do people who have good eyesight when young require glasses as they grow old?

(7) Color and Spectra

Guglielmo Marconi

"Copyright by Underwood & Underwood, N. Y."
Guglielmo Marconi (Italy). Inventor of wireless telegraphy.

Alexander Graham Bell

"Copyright by Underwood & Underwood, N. Y."
Alexander Graham Bell, Washington, D. C. Inventor of the telephone.

[Pg 432]
[Pg 433]
399. Color.?Much of the pleasure experienced in gazing at beautiful objects is due to the color shown by them. The blue sky, the green grass, and the varied tints of flowers, and of the rainbow all excite our admiration The study of color begins naturally with the production of the spectrum, the many-colored image upon a screen produced by passing a beam of light through a prism. The spectrum is best shown when the light enters by a narrow slit (Fig. 400). The spectrum was first produced by Sir Isaac Newton in 1675 by the means just described. The names usually given to the more prominent colors of the spectrum are violet, indigo, blue, green, yellow, orange, and red. The initials of these names, combined, spell vibgyor, a word without meaning except to assist in remembering the order of the colors in a spectrum. If the light that has passed through a prism is sent through a second prism placed in reverse position (see Fig. 401), the light passing through both prisms is found to be white. This experiment indicates that white light is composed of light of all colors.

Fig. 400.?Formation of the spectrum by a prism.

Fig. 401.?The colors of the spectrum recombine to form white light.

400. Dispersion.?The separation of the colors by a prism is called dispersion. In experimenting to find a[Pg 434] reason for dispersion, it has been learned that lights of different colors are of different wave lengths. Color in light is therefore analogous to pitch in sound. We hear through many octaves, but we see through about one octave. That is, the shortest visible waves of violet light are about 0.000038 cm. in length while the longest visible red rays are 0.000076 cm., or the longest visible light waves are about twice the length of the shortest visible ones. It appears from the evidence of experiments upon dispersion that light waves of different lengths are refracted differently. This causes the images formed by refraction through simple glass lenses to be fringed with color and to lose some of their sharpness and definiteness of outline, since the violet light is brought to a focus sooner than the red. (See Fig. 402.) This seriously affects the value of such lenses for optical purposes. Fortunately it is found that different kinds of glass have a different rate of dispersion for the same amount of refraction.

Fig. 402.?Violet light comes to a focus sooner than red.

401. The Achromatic Lens.?The existence of these different kinds of glass makes possible a combination of lenses in which dispersion is entirely overcome with the loss of only about one-half of the refraction. Such a combination is shown in Fig. 403. It is called an achromatic lens, since images formed by it are not colored but white (a = without, chroma = color). The achromatic lens consists of a double convex lens of crown glass combined with a plano-concave lens of flint glass. Achromatic lenses are used in all high-grade optical instruments such as[Pg 435] telescopes and microscopes. The colored images that are sometimes seen in cheap opera glasses show the result of not using achromatic lenses.

Fig. 403.?An achromatic lens. C is of crown glass; F, of flint glass.

402. The Color of Bodies.?Project the spectrum of sunlight upon a white surface in a darkened room.

Now place in different parts of the spectrum objects of various colors. Red objects will show brilliant red when at the red end of the spectrum but look black at the blue end, while blue objects appear blue only at the blue end.

These facts indicate that the color of an object depends upon two things: (a) the light that falls upon it and (b) the light which it sends to the eye. A black surface absorbs all color while a white one reflects all wave lengths to the eye in the same proportion that they come to it. A white object will appear red in red light, and blue in blue light since it reflects both of these. A colored object reflects light of its own color but absorbs all others. The color then of a body is due to the light which it does not absorb, but which comes from it to the eye.
403. The color of transparent bodies, such as colored glass, is due to the presence of a dye or pigment contained in the body. This pigment absorbs a part of the light, the part transmitted giving the color. This may be shown by holding a sheet of colored glass in a beam of light either before or after it has passed through a prism. Some colors, as red, may be found to be nearly pure, only the red passing through, while green glass often transmits in addition to the green some yellow and some red light.
[Pg 436]
404. Complementary Colors.?If two prisms are placed in reversed position near each other (see Fig. 401), a beam of light dispersed by one is recombined into white light by the other. If now a card is held between the two prisms so as to cut off some of the colored light, say the red, the remaining light will be found to form a greenish blue. If the card is removed, the light becomes white again. That is, red and peacock blue light together form white. Any two colors that together form white light are called complementary. Other complementary colors are light yellow and blue, green and crimson, orange and greenish blue, violet and greenish yellow. We must not confuse the combining of colors (light) and the combining of pigments, the latter consisting of bodies that absorb light. Yellow pigment absorbs all but yellow and some green, while blue pigment absorbs all but blue and some green. Mixing these two pigments causes the absorption of all colors but green. Blue and yellow paint mixed produce green, while blue and yellow light give white.
405. The solar spectrum, as the spectrum of sunlight is called, may be observed in the rainbow. The latter is produced through the dispersion of light by spherical raindrops. Its formation may be imitated by sending a small circular beam of light through a screen against a round glass flask filled with water. (See Fig. 404.) The light passes through the water and is dispersed when it enters and when it leaves, producing a color upon the screen at R-V. The course of the light within the drop is indicated in Fig. 405. The violet ray comes to the eye more nearly horizontal and is therefore below red, as we look at the rainbow.
406. Fraunhofer Lines.?Some of the most important features of the solar spectrum are not seen in the rainbow or in the band of light usually observed upon a screen.[Pg 437] By the use of a narrow slit and a convex lens to carefully focus the slit upon a white screen it is seen that the solar spectrum is crossed by many dark lines. These are called Fraunhofer lines, to honor the German scientist who in 1814 first accurately determined their position. Two experiments with a spectroscope will help to make clear the meaning of the Fraunhofer lines.

Fig. 404.?A rainbow formed by a beam of light striking a flask of water.
Fig. 405.?The course of a beam of light within a drop of water.

[Pg 438]
407. The Spectroscope and Its Uses.?The spectroscope (Fig. 406) is an instrument for observing spectra. It consists of a prism, a slit, and a convex lens T for focusing an image of the slit accurately upon a screen (Fig. 407) where the spectrum is observed through the eyepiece E.

Fig. 406.?The spectroscope.

(A) A Bunsen flame is placed in front of the slit and a heated platinum wire which has been dipped in common salt or some sodium compound placed in the Bunsen flame; the latter becomes yellow and a vivid yellow line is observed on the screen in the spectroscope. Other substances, as barium and strontium salts, when heated to incandescence in the Bunsen flame, give characteristic bright lines. In fact each element has been found to have its own characteristic set of colored lines. This fact is made use of in spectrum analysis, by which the presence of certain elements in a substance can be definitely proved upon the appearance of its particular lines in the spectrum.

Fig. 407.?Diagram of a spectroscope.

Fig. 408.?The bright line spectrum of iron and its coincidences with some of the dark lines of the solar spectrum.

(B) If light from, for example, an arc light is sent over a gas flame containing sodium vapor, a dark line appears in[Pg 439] the spectrum?in the exact position in which the yellow sodium line appeared. It seems that the sodium vapor removes from white light the same wave lengths that it itself produces. This absorption is supposed to be due to sympathetic vibration; just as a tuning fork is set in vibration by the waves of another fork in unison with it, at the same time absorbing the wave energy, so in the gas flame the sodium particles absorb the wave motion of the same vibration rate as that emitted by them. The fact that the spectrum of sunlight contains a great many dark lines is believed to indicate that the sun is surrounded by clouds formed by the vaporization of the various substances in the sun itself. By comparing the dark lines of[Pg 440] the solar spectrum with the bright-line spectra of various substances found in the earth, such an exact correspondence of the lines is found that the presence of the vapor of these substances about the sun is considered proved. (See Fig. 408 which shows the exact correspondence between the bright-line spectrum of iron vapor and the dark lines appearing in a portion of the sun's spectrum.) The spectra of the stars also contain certain dark lines. Thus the presence of the corresponding substances in distant stars is considered as determined.
408. Theory of Color Vision.?By combining light of the three colors red, green and blue-violet in proper proportions, it has been found possible to produce any color effect, even white. This leads to the conclusion that in the retina of the eye are three different kinds or sets of sensitive nerve endings, sensitive respectively to red, to green, and to blue light. This idea is given corroboration by some facts of color blindness. Thus some persons have no sensation of red, this color not being distinguished from green. Others are color blind to green or blue. It is supposed that in color blind persons one of the sets of nerve endings sensitive to one of these three colors is lacking.
409. Three-color Printing.?Since all colors may be produced by mixing the three colors, light red, green, and blue-violet, these are called the three primary colors. The so-called primary pigments or paints are simply the complements of the three primary colors. They are, in order, peacock blue, crimson, and light yellow. The three pigments when mixed yield black, since combined they absorb all kinds of visible light. The process of three-color printing, now so generally employed in printing colored pictures for books, calendars, etc., consists in combining upon white paper three colored impressions,[Pg 441] using successively the three primary pigments (yellow, crimson and blue) from plates prepared as follows:
Three photographs of a given colored object are taken, each through a different sheet of gelatine called a filter, stained the color of one of the primary colors. From these photographs half-tone blocks are made in the usual way. The colored picture is made by carefully superposing impressions from these blocks, using in each case an ink whose color is the complement of the "filter" through which the original picture was taken. An illustration of the process is given upon the plate in the frontispiece of this book.

Important Topics

1. Color, due to wave length; dispersion by prism, sphere in rainbow, complementary colors, color of opaque and transparent bodies.
2. Spectra, solar; formation of rainbow; bright-line spectra, how formed, how used; dark-line, how formed, used.
3. Theory of color vision. Three color printing.

Exercises

1. How does a white flower look when viewed through a blue glass? Through a red glass? Through a red and blue glass at the same time?
2. Why does a red ribbon appear black when seen by blue light and red when seen by red light?
3. In what part of the sky must you look to see a rainbow in the morning? In the afternoon? Explain.
4. How would you arrange two similar prisms so as to produce double the deviation produced by one?
5. The color of an object depends upon what two things?
6. What kind of a spectrum should moonlight give? Why?
7. A mixture of green and red lights gives a sensation of yellow. Can you suggest why a mixture of blue and yellow lights gives the sensation of white?
[Pg 442]

(8) Nature of Light, Interference, Polarization

410. The Corpuscular Theory.?The theory of the nature of light that was most generally accepted until about the year 1800, held that light consists of streams of minute particles, called corpuscles, moving at enormous velocities. This corpuscular theory was in accord with the facts of reflection and the rectilinear motion of light, but was abandoned after the discovery of the interference of light, as it could not account for the latter phenomenon.
411. The Wave Theory of Light.?The theory that light is a form of wave motion was first advanced by Huygens, a Dutch physicist, in the seventeenth century. This theory was opposed at the start since (A) no medium was known to exist which would convey wave motion through space, as from the sun to the earth, and (B) the rectilinear motion of light was unlike that of any other form of known wave motions, such as that of water or of sound waves which are able to bend around corners. In answer to the first objection, Huygens assumed the presence of a medium which he named ether, while the second objection has been completely overcome during the past century by the discovery that light may deviate from a straight line. It is now known that the excessive shortness of light waves is the reason for its straight-line motion. Further, long ether waves, as those of wireless telegraphy, are found to bend around obstacles in a manner similar to those of water or sound.

Fig. 409.?Two plates pressed together by a screw clamp.
Fig. 410.?Illustrating the interference of light by a thin film of air.

412. The interference of light is one of the phenomena for which the wave theory offers the only satisfactory explanation. Interference of light may be shown by taking two pieces of plate glass and forcibly pressing them together by a screw clamp, as shown in Fig. 409. After a certain pressure has been reached, colored rings will appear[Pg 443] about the compressed spot when viewed by light reflected from the upper surface of the glass. If light of one color, such as that transmitted by red glass, falls upon the apparatus, the rings are seen to be alternately red and dark bands. The explanation of this phenomenon according to the wave theory is as follows: The two sheets of glass, although tightly pressed together, are separated in most places by a thin wedge of air (see Fig. 410), which represents in an exaggerated form the bending of the plates when pressed by the clamp. Several waves are represented as coming from the right and entering the glass. Now the wave moving from R to the plates has some of its light reflected from each glass surface. Consider the two portions of the wave reflected at each of the surfaces between the plates, i.e., from the two surfaces of the wedge of air. If the portion of the wave reflected from the second surface of the air wedge combines with that reflected from the first surface, in the same phase as at C, the two reflected waves strengthen each other. While if the two reflected portions of the wave meet in opposite phases as at A and B, a decrease or a complete extinction of the light results.[Pg 444] This is called interference. If light of one wave length is used, as red light, the regions of reinforcement and interference are shown by red and dark rings, while if white light is used, the ring where red light interferes, yields its complementary color, greenish blue. Where interference of greenish blue occurs, red is found, etc. Many phenomena are due to interference, such as (A) the color of thin films of oil on water, where the portions of light reflected from the two surfaces of the oil film interfere resulting in the production of color; (B) the color of soap bubbles. When first formed, soap-bubble films are not thin enough to show interference well, but as the bubbles increase in size or become thinner on standing, the conditions for interference are reached and, as the film becomes thinner, a regular succession of colors is noticed.
413. Differences Between Light and Sound.?Among the important differences between light and sound that have been considered are the following: the former are (a) waves in the ether, (b) of very short wave length, and (c) their motion is in straight lines. Another difference (d) is in the mode of vibration.
Sound waves are longitudinal, while light waves are transverse. Light waves consist of vibrations of the ether at right angles to the line of motion. To illustrate the reasoning that has led to this conclusion, suppose a rope to be passed through two vertical gratings. (See Fig. 411, 1.) If the rope be set in transverse vibration by a hand, the waves produced will readily pass through to the gratings P and Q and continue in the part extending beyond Q. If, however, Q is at right angles to P, no motion will be found beyond Q. Now if a stretched coiled spring with longitudinal vibrations should take the place of the rope, it is evident that the crossed position of the two gratings would offer no obstacles to the movement of the vibration.[Pg 445] In other words, crossed gratings offer no obstruction to longitudinal vibrations, while they may completely stop transverse vibrations.

Fig. 411.?Transverse waves will pass through both gratings in (1) where the openings in the two gratings are at right angles. The waves passing P are stopped by Q (2).Fig. 411.?Transverse waves will pass through both gratings in (1) where the openings in the two gratings are at right angles. The waves passing P are stopped by Q (2).

Fig. 412.?Effect of tourmaline crystals on light.

414. Polarization of Light.?It is found that two crystals of tourmaline behave toward light just as the two gratings behave with respect to the transverse waves of the rope. Thus, if a small opening in a screen is covered with a tourmaline crystal, light comes through but slightly diminished in intensity. If a second crystal is placed over the first one so that the two axes are in the same direction as in Fig. 412P, light is as freely transmitted through the second crystal as through the first, but if the crystals are crossed (Fig. 412S) no light passes the second crystal. This experiment shows that the light which has passed through one tourmaline crystal will pass through another only when the latter is held in a certain position, hence it is believed that a tourmaline crystal is capable of transmitting[Pg 446] light that is vibrating in one particular plane. The direct conclusion from this is that light waves are transverse rather than longitudinal. The experiment just described illustrates what is called polarization of light. The beam that after passing through a (Fig. 412) is unable to pass through b, if the two axes are crossed, is called a polarized beam. The conclusion that light waves are transverse is therefore based upon the phenomenon of the polarization of light. This was first discovered by Huygens in 1690.

Important Topics

1. Interference of light: evidence, reasoning involved, illustration.
2. Polarization of light: evidence, reasoning involved.
3. Nature of light, differences between sound and light.

Exercises

1. Make a list of the differences between sound and light and state briefly the evidence upon which the knowledge of these differences is based.
2. Why will a thickness of film that will produce interference of red light be different from that producing interference for green or blue?
3. Using the formula n = v/l compute the vibration rate for violet light if its wave length is considered as 0.00004 cm.
4. Explain how the fact of polarization affects the wave theory of light.
5. Show how it is possible by comparing the spectrum of the sun with that of a star to tell whether the star is approaching or receding from the earth.

Review Outline: Light

Light; speed, source, medium.
Straight Line Motion; shadow, umbra, penumbra, eclipse, image.
Photometry; Law of intensity, candle power, foot-candle.
Mirrors; Law of reflection; image?real, virtual; plane, curved, parabolic, mirrors.
[Pg 447]
Refraction; cause and effects; plate, prism, lens; total reflection.
Lenses; six forms, principal focus, center, lens equation, 1/F = 1/D_o + 1/D_i.
Optical instruments; eye, defects and correction, camera, microscope, etc.
Spectra; 3 kinds, dispersion, production of color effects, spectroscope, uses.
Nature of Light; wave theory, interference, polarization, significance.

➨ Chapter XVII. Invisible Radiations

Search This Blog

Exercise Pro