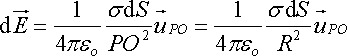Exercise Pro

∎ Return to the exercise   We Can modeled within a cavity hollowed out of the sphere R as the superposition of a charged sphere of radius a volume density - ρ   of center O2 and a full sphere of volume density ρ of radius R and center O1. The principle of superposition is applied at a point M of the cavity: field created by the distribution ρ field created by the distribution - ρ Symmetry and invariance of each source can be concluded for each radial field : Using the Gauss, taking for each distribution a sphere of radius r and center Oi closed surface and passing through the point M.   We get : The field is uniform at any point inside the cavity. ∎ Return to the exercise ∎ Back to the list of electromagnetism corrected exercises

∎ See the solution Consider a uniformly charged surface plane which is practiced in an empty hole of radius R and fillers. Determine the electrostatic field at a point M of the axis of the hole. We note s the surface density loads.   ∎ See the solution   ∎ See the list of electromagnetism corrected exercises

►Back to exercise 1. O electrostatic field. The z axis is the axis of symmetry of load distribution. Field O is carried by this axis. Consider a surface element of the half sphere centered at a point P. Elemental electrostatic field created by this element to the point O of the axis Oz is expressed as: Only the projection of this vector onto axis Oz contributes to the field at the point O: The field component O is: 2. Electrostatic Field in M. The z axis is the axis of symmetry of load distribution. The field M is carried by this axis. Consider a surface element of the half sphere centered at a point P. Elemental electrostatic field created by this element at the point M of the axis Oz is expressed as: Only the projection of this vector onto axis Oz contributes to the field at point M: Gold : and where: By integration: Gold : ...

► E lectrostatic field . ∎ 1. Field the center of a ring having an opening. (The solution ) ∎ 2. Field created by a hemisphere surface charge. ( The Solution ) ∎ 3. field created by a portion of a cone. (The Solution ) ∎ 4. Field created by a disc at a point on its axis. (The Solution ) ∎ 5. electrostatic field created by an electrified segment. (The solution ) ∎ 6. Electrostatic field created by a hemisphere surface charge. ( The solution ) ∎ 7. Electric field on the axis of a system (-q, + q) ( the solution )     ►2. Electrostatic potential . ∎ 1. The potential field created by a disc at a point on its axis of revolution . ~ ∎ ( The Solution ) ∎ 2. Potential and field created by a charged hemisphere surface ~ ∎ ( the solution ) ∎ 3. The potential created by a portion of a cone ~ ∎ ( The solution ) ∎ 4. Field Lines ► 3. Gauss Theorem ∎ 1. Hydrogen Atom ~ ∎ ( T he solution ) ∎ 2. Study of a cylindrical charge ...