Exercise Pro

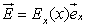
∎ Back to exercise   1. Field . Being a point M belonging to the Ox axis. The planes passing through this axis are planes of symmetry of the charge distribution, the direction of the electrostatic field is contained in all these plans: the direction of the field is carried by the axis Ox. On the other hand, the distribution is invariant for all translation parallel to the plane yOz. Therefore : The yOz plan is also a plane of symmetry of the charge distribution. Then E x (- x) = - E x (x). To determine the electric field, we apply the Gauss theorem considering as Gaussian surface  a cylinder of height 2x, with axis Ox and O its center . 2. Speed A charge q of the same charge of the layer is initially blocked by the layer to the point of abscissa x = 0. To cross this layer it is sufficient that the charge q reaches the plane yOz since beyond this level, it is pushed to the right. Applying the theorem of k...

►The solution A particle of charge q> 0 and  mass m   , arrives at x = - a with velocity v o perpendicular to an infinite plane layer ,  of thickness 2a and volume load r> 0 uniform. 1. To determine the characteristics of the electrostatic field vector inside the charged layer. 2. Determine the condition relating to v o to the load passes through the layer. ►See the solution   ►Voir list electromagnetism exercises  

► See the solution Considering a half sphere of center O, of radius R, uniformly charged on surface with the surface density σ. 1. Determine the electrostatic potential at a point M of the axis Oz of symmetry of this hemisphere. 2. Deduce the expression of the electrostatic field at that point Mr. 3. Determine the potential and the electrostatic field on O. ( think for limited development). ► See the solution ► Back to the list of electromagnetism exercises

∎ Back to exercise 1. The potential at a point M of the axis. Consider a surface area element of the disk centered at a point P. The electrostatic potential created at a point M of the axis Oz is expressed as: Since r and θ variables are separated : For the calculation is performed following variable change: For : On the other hand : We get : Taking the zero potential at infinity is obtained: 2. Field at a point M of the axis. The z axis is axis of symmetry of the charge distribution. The field at a point M of the axis is carried by this axis: We must therefore calculate the derivative of the function . We have: x = y where sh As   ∎ Back to exercise ∎ Back to the list of electromagnetism exercises  

► E lectrostatic field . ∎ 1. Field the center of a ring having an opening. (The solution ) ∎ 2. Field created by a hemisphere surface charge. ( The Solution ) ∎ 3. field created by a portion of a cone. (The Solution ) ∎ 4. Field created by a disc at a point on its axis. (The Solution ) ∎ 5. electrostatic field created by an electrified segment. (The solution ) ∎ 6. Electrostatic field created by a hemisphere surface charge. ( The solution ) ∎ 7. Electric field on the axis of a system (-q, + q) ( the solution )     ►2. Electrostatic potential . ∎ 1. The potential field created by a disc at a point on its axis of revolution . ~ ∎ ( The Solution ) ∎ 2. Potential and field created by a charged hemisphere surface ~ ∎ ( the solution ) ∎ 3. The potential created by a portion of a cone ~ ∎ ( The solution ) ∎ 4. Field Lines ► 3. Gauss Theorem ∎ 1. Hydrogen Atom ~ ∎ ( T he solution ) ∎ 2. Study of a cylindrical charge ...