Solution : Potential field created by a disc at a point on its axis of revolution - electrostatic potential - Corrected exercises electromagnetism



1. The potential at a point M of the axis.
Consider a surface area element of the disk centered at a point P. The electrostatic potential created at a point M of the axis Oz is expressed as:
Since r and θ variables are separated :
For the calculation is performed following variable change:
For :
On the other hand :
We get :
Taking the zero potential at infinity is obtained:
2. Field at a point M of the axis.
The z axis is axis of symmetry of the charge distribution. The field at a point M of the axis is carried by this axis:
We must therefore calculate the derivative of the function .
We have: x = y where sh
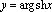
As






 



Comments

Post a Comment

Popular posts from this blog

Solution : Study of a spherical inhomogeneous distribution - Corrected Exercises Gauss Theorem

Image
∎ Return to the exercise 1. Expression of the electrostatic field.   All the planes containing the center O of the sphere and the point P are the load distribution of planes of symmetry. The electric field must belong simultaneously to all of these plans, it is therefore carried by their intersection which is the line OM.  we obtain.: As this distribution has a rotational invariance around the point O, the electric field does not depend on the angular variables. This result does not depend on the position of this point P. We choose a Gaussian surface centered in O and radius r. The Gauss theorem is: Then there are two regions of space: ● For r <R (one can put an equal sign here because the density distribution is what ensures the continuity of the normal component (here radial) of the electrostatic field). For the domestic load: Is obtained by applying the Gauss theorem: ...
Read more

TRADITIONAL INDUSTRIAL ARTS DESIGN - PRACTICAL METHODS FOR STUDENTS, TEACHERS, AND CRAFTSMEN - BY WILLIAM H. VARNUM 1916

Image
CONTENTS CHAPTER PAGE I. Divisions of Industrial Arts Design 7 II. The Primary Mass and Its Proportions 13 III. Horizontal Major Divisions of the Primary Mass 19 IV. Vertical Major Divisions of the Primary Mass 33 V. Appendages and the Rules Governing Them 43 VI. Enrichment of the Contours or Outlines of Designs in Wood 57 VII. Enrichment of the Contours or Outlines of Designs in Clay 77 VIII. Enrichment of the Contours or Outlines of Designs in Base and Precious Metals 87 IX. Surface Enrichment of Small Primary Masses in Wood 99 X. Surface Enrichment of Small Primary Masses in Wood. (Continued) 117 XI. Surface Enrichment with Minor Subdivisions of Lar...
Read more

ELECTRICITY IN LOCOMOTION - BOOK

►Early Tramroads and Railways ►The Birth of Electric Traction   ►The Essential Advantages of Electric Traction on Tramways  ►The Mechanism of an Electric Tramcar: the Overhead System  ►Conduit and Surface-Contact Tramway Systems  ►The Backwardness of Electric Traction in Great Britain ►Electric Tramway Stagnation. The Trolley Omnibus   ►Regenerative Control  ►Accumulator Electric Traction. The Electric Automobile ►Petrol-Electric Vehicles and main Marine Propulsion by Electricity  ►The Pioneer Electric Railways ►Electric Railways from the Engineering Point of View  ►Electric Traction on Main Line Railways  ►Curiosities of Electric Traction  By ADAM GOWANS WHYTE, B.Sc.
Read more