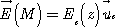Exercise Pro

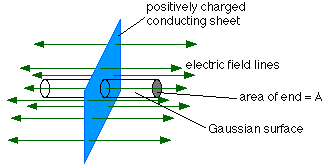
∎ 1. Hydrogen Atom ~ ∎ ( The solution ) ∎ 2. Study of a cylindrical charge distribution. ~ ∎ ( The solution ) ∎ 3. Crossing a charged layer ~ ∎ (The solution ) ∎ 4. Field on the axis of a circular opening of a plan. ~ ∎ ( The Solution ) ∎ 5. Field in a spherical cavity. ~ ∎ ( The solution ) ∎ 6. Research Officer of the electrostatic field generated by a half-charged sphere surface. ∎ 7. Study of a spherical inhomogeneous distribution. ~ ∎ ( The Solution ) ∎ 8. field in the vicinity of the axis of a uniformly charged hoop ~ ∎ ( The Solution ) ∎ 9. uniform volumetric density between two planes ► See the list of electromagnetism corrected exercises

Consider two infinite planes x = - a and x = a. The space between the two planes has a volume density of uniform and constant ρ loads. For x> a and x <- a, it reigns on vacuum . Show that at any point of space, the electrostatic field of this distribution can be written . Expressing Ex for the different parts of space and plot the Ex a function of x. Determine for each region the potential V (x) adopting V (0) = 0. Draw the graph of V (x) in terms of x. It is assumed that a approaches 0 and that the multiplication  ρa remains finite. Set an areal density limit load and look for Ex   on a classic result. ► See solution ► See the list of electromagnetism exercises

► Return to the exercise 1. electrostatic field at a point on the axis of the ring. The planes containing the axis Oz are symmetry planes of load distribution  ; at a point M of this axis, the direction of the electrostatic field must belong to each plan so they intersect: with So: where: As the plane containing the hoop is also a load distribution of the symmetry plane was at a point M' is symmetrical of M from the hoop:       with: Finally, we get to any point on the axis of the hoop: 2. Field in a spot close to the axis. We work in cylindrical coordinates. For any point M of space, the plane containing the point M and the axis Oz is a plane of symmetry of the charge distribution. The field is contained in the plan. Furthermore as there invariance of the charge distribution by rotation about axis Oz we ...

►See the solution A hoop of radius R, center O, carries the linear  uniform load λ . 1.         Determining the expression of the electrostatic field created by the hoop at a point M of the axis Oz. 2.         It is proposed to calculate now the field in the vicinity of the axis of the hoop. Using a Gaussian surface having the form of a small Oz axis of cylinder of radius r and of length dz and by assuming that E z (r, z) = E z (axis) to a point close to the axis, show that the radial component of the field is related to the value of the field axis by: Determine at a point closest to the axis. ►See the solution ► See the list of electromagnetism exercises

∎ Return to the exercise 1. Expression of the electrostatic field.   All the planes containing the center O of the sphere and the point P are the load distribution of planes of symmetry. The electric field must belong simultaneously to all of these plans, it is therefore carried by their intersection which is the line OM.  we obtain.: As this distribution has a rotational invariance around the point O, the electric field does not depend on the angular variables. This result does not depend on the position of this point P. We choose a Gaussian surface centered in O and radius r. The Gauss theorem is: Then there are two regions of space: ● For r <R (one can put an equal sign here because the density distribution is what ensures the continuity of the normal component (here radial) of the electrostatic field). For the domestic load: Is obtained by applying the Gauss theorem: ...

►Voir solution Considering in the vacuum a sphere of radius R, the center O, with a volume charge distribution : and k are constants and 1. Determine the expression of the electrostatic field at any P in space. Note OP = r. 2. Show that within the sphere, the electrostatic field has a maximum for a ratio r / R given. Calculate the value of k in the case where the field is extremum for r / R = 1/2 ►Voir solution ∎ See the list of electromagnetism corrected exercises  

Considering a half sphere of center O, of radius R, uniformly charged surface with the surface density s. Determine, using only the symmetries The invariance, the Gauss theorem and the superposition principle the direction of the electrostatic field at any point M of the diametrical plane.   ∎ solution soon ∎ See the list of electromagnetism exercises

∎ Return to the exercise   We Can modeled within a cavity hollowed out of the sphere R as the superposition of a charged sphere of radius a volume density - ρ   of center O2 and a full sphere of volume density ρ of radius R and center O1. The principle of superposition is applied at a point M of the cavity: field created by the distribution ρ field created by the distribution - ρ Symmetry and invariance of each source can be concluded for each radial field : Using the Gauss, taking for each distribution a sphere of radius r and center Oi closed surface and passing through the point M.   We get : The field is uniform at any point inside the cavity. ∎ Return to the exercise ∎ Back to the list of electromagnetism corrected exercises